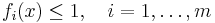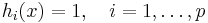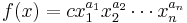Geometric programming
A geometric program (GP) is an optimization problem of the form
- Minimize
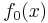 subject to
subject to
- where
 are posynomials and
are posynomials and  are monomials.
are monomials.
In the context of geometric programming (unlike all other disciplines), a monomial is defined as a function 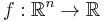 with
with 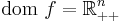 defined as
defined as
where 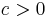 and
and 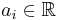 .
.
GPs have numerous application, such as components sizing in IC design[1] and parameter estimation via logistic regression in statistics. The maximum likelihood estimator in logistic regression is a GP.
Contents |
Convex form
Geometric programs are not (in general) convex optimization problems, but they can be transformed to convex problems by a change of variables and a transformation of the objective and constraint functions. In particular, defining 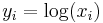 , the monomial
, the monomial 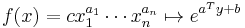 , where
, where 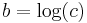 . Similarly, if
. Similarly, if  is the posynomial
is the posynomial
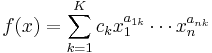
then 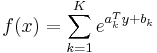 , where
, where 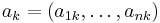 and
and 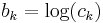 . After the change of variables, a posynomial becomes a sum of exponentials of affine functions.
. After the change of variables, a posynomial becomes a sum of exponentials of affine functions.
References
- Richard J. Duffin; Elmor L. Peterson, Clarence Zener (1967). Geometric Programming. John Wiley and Sons. pp. 278. ISBN 0471223700.
External links
- S. Boyd, S. J. Kim, L. Vandenberghe, and A. Hassibi, A Tutorial on Geometric Programming
- S. Boyd, S. J. Kim, D. Patil, and M. Horowitz Digital Circuit Optimization via Geometric Programming